Remember anything multiplied by zero is zero . It is best to learn tables up to 50 and even some fraction tables like half times 2 equals one etc.

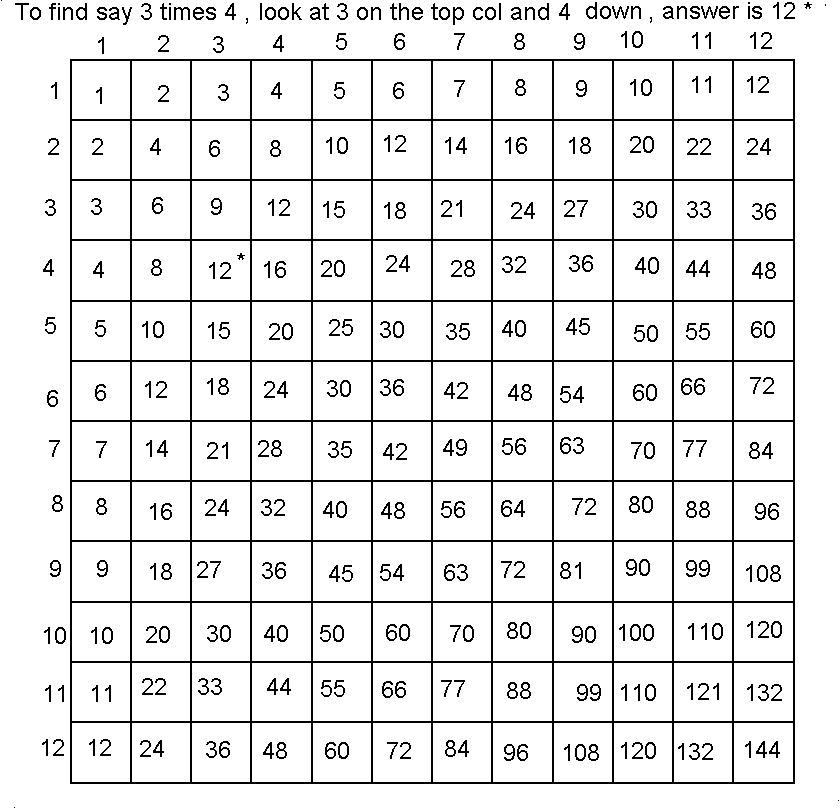
Here is the table till 12 - one must really learnt it and memorise it . It may take a week but is worth it.

2+2 = 4 This operation is useful to know as it is all a computer can do ! .

7-3 = 4

x or * sign
This really is addition carried out many times . For eg 4 x 3 means add 4 to itself 3 times ie 4+4+4 equals 12 . When we ask a computer to multiply many times , it actually adds it very fast like in this example.

Really means how many times one number has to be added to itself to give the other number . For example 12 /4 =3 .

What is the number that when multiplied by itself gives the other number . For example 4 is the square root of 16.

What is the number when multiplied by itself three times gives the other number ? For example 3 is the cube root of 27 . Similarly y is the nth root of b if when y is multiplied by itself n times gives b .

Suppose we were told that a train goes 5 km in one second . How far has it gone in three ? The answer we know is 15 . The way we write it in Maths is

5 x 3 = 15

Now 5 is the constant speed while the number of seconds varies with time . We can designate the unknown with a letter say X . So we can write an equation

5 x X = ? and give it our friends and they can put in any value of X . For example in 7 seconds the distance gone would be 5x X ie 5 x 7 = 35 km . Since the distance also varies we could give it another letter Y . So our equation becomes

5 x X = Y .

If we are given a value for X say 9 seconds we can get Y as 45 km . Also if we are told that the train has gone 100 km we can work out from

5 x X = 100 that it must have been going 20 seconds .

X , Y , Z etc are called unknown variables . Note we need to know either the speed or distance to calculate the other .

So one equation only lets us solve for one unknown. We will use * as the multiplication sign as otherwise x and X can be confused. So the above equation becomes

5 * x = y

Lets look at another equation

8 + 4 = 12

If we subtract 4 from each side the equation still makes sense

8+4-4 = 12 - 4

8 = 8

So in other words we have taken 4 over to the other side and changed its sign from + in front to - from 8 + 4 = 12 to

8 = 12 -4

Similarly

12 / 3 = 4 we can take 3 over to the other side when the sign if front of it changes from divide ( /) to multiply ( * ) ie

12 = 4 * 3

So remember to leave just one unknown on one side we take all the others over and change their signs . For example

z + 8 = 15 to
z = 15- 8
z= 7

and if

y * 3 = 9
to y = 9 / 3
y = 3

To find two unkowns we need two equations.

For example

2 + x = y equation 1
2 * x =y -1 equation 2

In equation 2 taking -1 over to the other side
we get 2 * x + 1 = y equation 3

Now since equation 2 and 3 are both equal to y we can make them equal to each other .

So 2+ x = 2 * x + 1
Collecting all the x terms on one side

2 - 1 = 2x - x

So 1 = x

Having found x = 1 we put this value into equation 1 and we get 2 + 1 = y . so y = 3 . To check we put this value of y in equation 2 and we get 2 x 1 = 3 -2 and that is correct.

As an exercise write down 3 equations for x , y and z where you give known values to x , y and z and see if you can work them out .

Eg x + y + z = 12
x - y -z = - 2
x + 2y + z = 16

Answer in the next lesson .